مهندسی عمران-زلزله(محمدجواد خسرویانی)

مهندسی عمران-زلزله(محمدجواد خسرویانی)

مهندسی عمران-زلزله(محمدجواد خسرویانی)

Fourier Series Learning


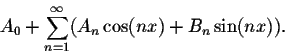
\begin{displaymath}A_0 + \sum_{n = 1}^{\infty} (A_n\cos(nx) + B_n\sin(nx)).\end{displaymath}

is called a Fourier series.
Since this expression deals with convergence, we start by defining a similar expression when the sum is finite.

Definition. A Fourier polynomial is an expression of the form

\begin{displaymath}F_n(x) = a_0 + \Big(a_1\cos(x) +b_1\sin(x)\Big)+ \cdots + \Big(a_n\cos(nx) + b_n\sin(nx)\Big)\end{displaymath}

which may rewritten as
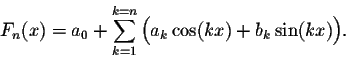
\begin{displaymath}F_n(x) = a_0 + \sum_{k= 1}^{k=n} \Big(a_k\cos(kx) + b_k\sin(kx)\Big).\end{displaymath}

The constants a0, ai and bi, $i=1,\cdots,n$, are called the coefficients of Fn(x).

The Fourier polynomials are $2\pi$-periodic functions. Using the trigonometric identities

\begin{displaymath}\begin{array}{lcr} \sin(mx)\cos(nx) &=&\displaystyle \frac{1}... ...e \frac{1}{2}\Big[\cos((m-n)x) - \cos((m+n)x) \Big] \end{array}\end{displaymath}

we can easily prove the integral formulas
(1)
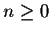for $n \geq 0$, we have
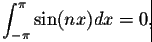\begin{displaymath}\int_{-\pi}^{\pi} \cos(nx)dx = 0,\;\;\;\mbox{and}\;\; \int_{-\pi}^{\pi}\sin(nx) dx = 0,\end{displaymath}

for n>0 we have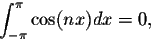
\begin{displaymath}\int_{-\pi}^{\pi} \cos(nx)dx = 0,\;\;\;\mbox{and}\;\; \int_{-\pi}^{\pi}\sin(nx) dx = 0,\end{displaymath}
(2)
for m and n, we have
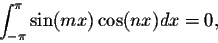
\begin{displaymath}\int_{-\pi}^{\pi} \sin(mx) \cos(nx)dx = 0,\end{displaymath}

(3)
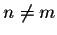for $n \neq m$, we have
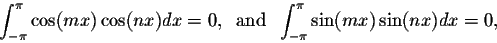
\begin{displaymath}\int_{-\pi}^{\pi} \cos(mx)\cos(nx)dx = 0,\;\;\mbox{and}\;\; \int_{-\pi}^{\pi}\sin(mx) \sin(nx)dx=0,\end{displaymath}

(4)
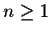for $ n \geq 1$, we have
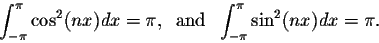
\begin{displaymath}\int_{-\pi}^{\pi}\cos^2(nx)dx = \pi,\;\;\mbox{and}\;\; \int_{-\pi}^{\pi} \sin^2(nx)dx = \pi.\end{displaymath}

Using the above formulas, we can easily deduce the following result:

Theorem. Let

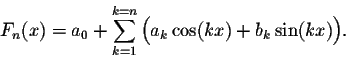
\begin{displaymath}F_n(x) = a_0 + \sum_{k= 1}^{k=n} \Big(a_k\cos(kx) + b_k\sin(kx)\Big).\end{displaymath}

We have
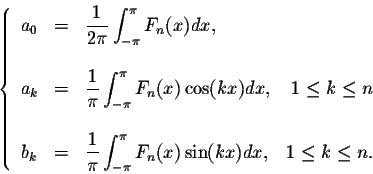
\begin{displaymath}\left\{\begin{array}{lclr} a_0 &=&\displaystyle \frac{1}{2\pi... ...\pi} F_n(x) \sin(kx)dx,& 1 \leq k \leq n.\\ \end{array}\right.\end{displaymath}

This theorem helps associate a Fourier series to any $2\pi$-periodic function.

Definition. Let f(x) be a $2\pi$-periodic function which is integrable on $[-\pi, \pi]$. Set

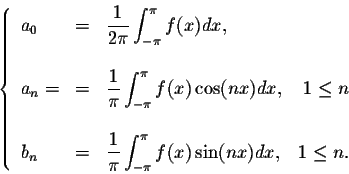
\begin{displaymath}\left\{\begin{array}{lclr} a_0 &=& \displaystyle \frac{1}{2\p... ..._{-\pi}^{\pi} f(x) \sin(nx)dx,& 1 \leq n.\\ \end{array}\right.\end{displaymath}

The trigonometric series
\begin{displaymath}a_0 + \sum \Big(a_n\cos(nx) + b_n\sin(nx)\Big)\end{displaymath}

is called the Fourier series associated to the function f(x). We will use the notation
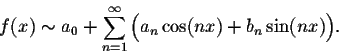
\begin{displaymath}f(x) \sim a_0 + \sum_{n=1}^{\infty} \Big(a_n\cos(nx) + b_n\sin(nx)\Big).\end{displaymath}

Example. Find the Fourier series of the function

\begin{displaymath}f(x) = x, \;\;\; -\pi \leq x \leq \pi.\end{displaymath}

Answer. Since f(x) is odd, then an = 0, for $n \geq 0$. We turn our attention to the coefficients bn. For any $ n \geq 1$, we have
\begin{displaymath}b_n = \frac{1}{\pi} \int_{-\pi}^{\pi} x \sin(nx)dx = \frac{1... ...\frac{x\cos(nx)}{n} + \frac{\sin(nx)}{n^2}\right]^{\pi}_{-\pi}.\end{displaymath}

We deduce
 
\begin{displaymath}b_n = -\frac{2}{n}\cos(n\pi) = \frac{2}{n}(-1)^{n+1}.\end{displaymath}
Hence
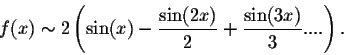
\begin{displaymath}f(x) \sim 2\left(\sin(x) - \frac{\sin(2x)}{2} + \frac{\sin(3x)}{3} ....\right).\end{displaymath}



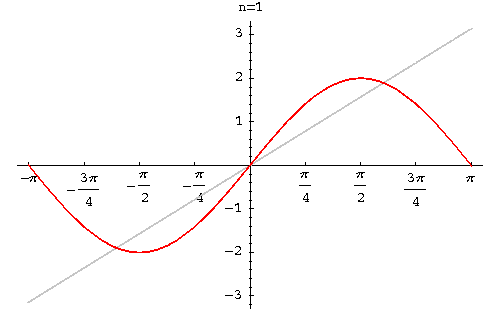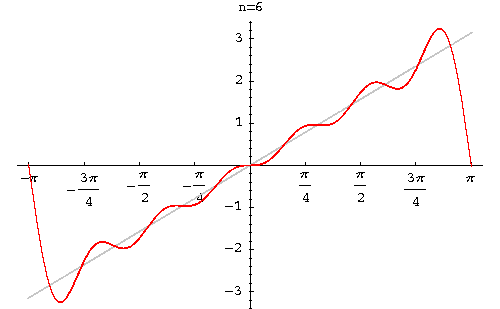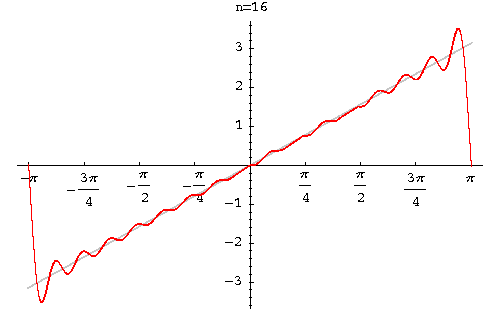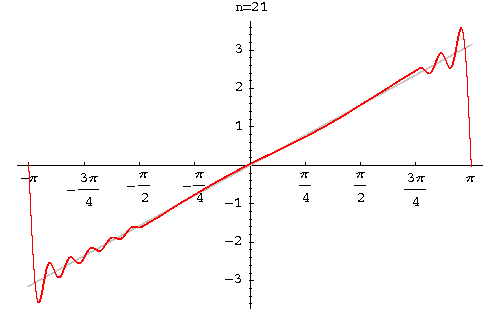Example. Find the Fourier series of the function

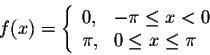
\begin{displaymath}f(x) = \left\{ \begin{array}{lll} 0,& -\pi \leq x < 0\\ \pi, & 0 \leq x \leq \pi \end{array} \right.\end{displaymath}

Answer. We have
\begin{displaymath}a_0 = \frac{1}{2\pi}\left(\int_{-\pi}^{0} 0dx + \int_{0}^{\pi... ...\;\;\; a_n = \int_{0}^{\pi} \pi\cos(nx)dx = 0, \;\;\; n \geq 1,\end{displaymath}

and
\begin{displaymath}b_n = \int_{0}^{\pi} \pi\sin(nx)dx = \frac{1}{n}(1-\cos(n\pi)) = \frac{1}{n}(1-(-1)^n).\end{displaymath}

We obtain b2n = 0 and
\begin{displaymath}b_{2n+1} =\frac{2}{2n+1}.\end{displaymath}

Therefore, the Fourier series of f(x) is
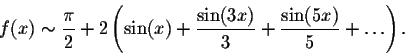
\begin{displaymath}f(x) \sim \frac{\pi}{2} + 2 \left(\sin(x) + \frac{\sin(3x)}{3} + \frac{\sin(5x)}{5}+\ldots\right).\end{displaymath}

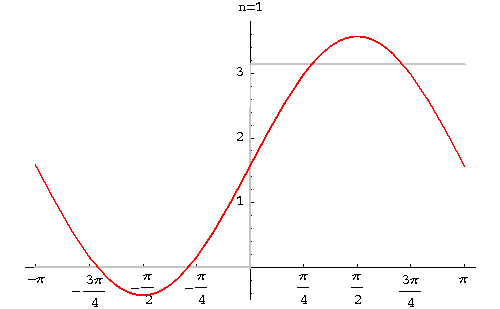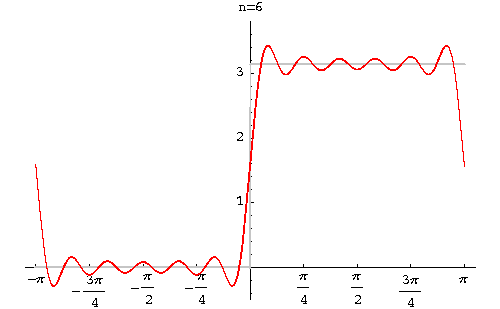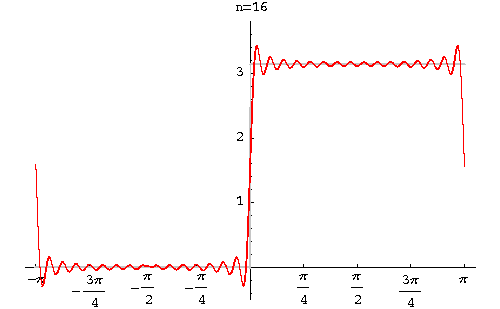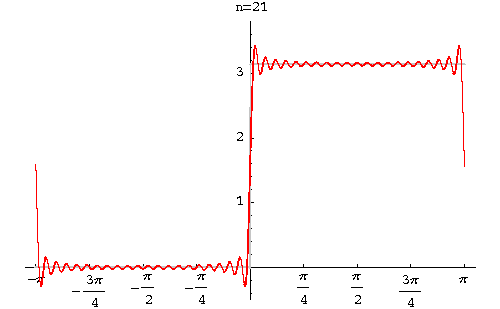
Example. Find the Fourier series of the function function

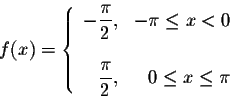
\begin{displaymath}f(x) = \left\{ \begin{array}{rrr} -{\displaystyle \frac{\pi}... ...ystyle \frac{\pi}{2}}, & 0 \leq x \leq \pi \end{array} \right.\end{displaymath}

Answer. Since this function is the function of the example above minus the constant $\displaystyle \frac{\pi}{2}$. So Therefore, the Fourier series of f(x) is
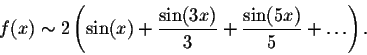
\begin{displaymath}f(x) \sim 2 \left(\sin(x) + \frac{\sin(3x)}{3} + \frac{\sin(5x)}{5}+\ldots \right).\end{displaymath}

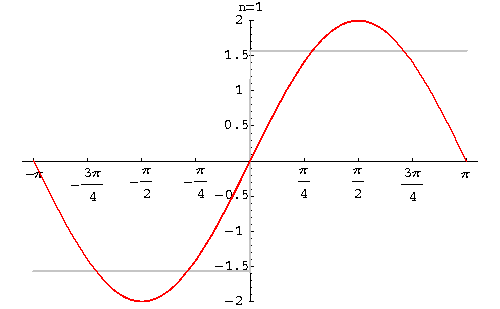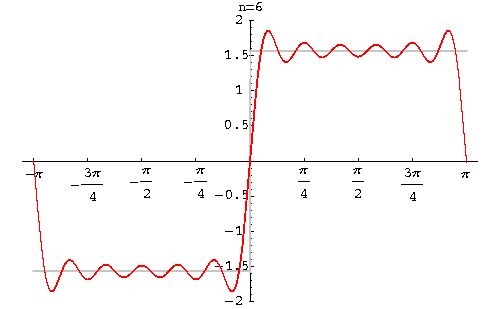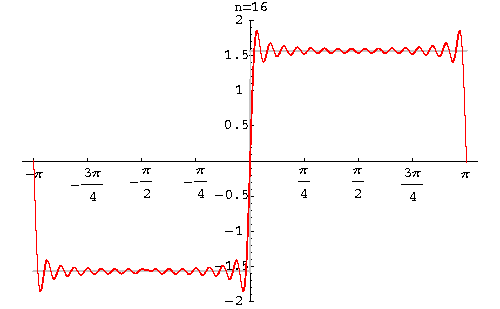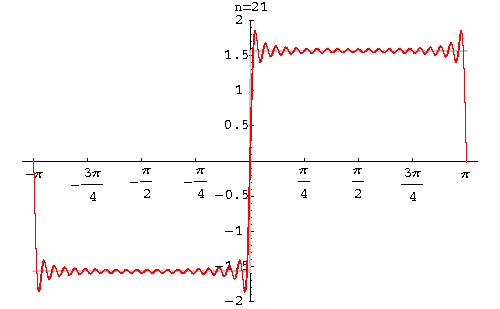
Remark. We defined the Fourier series for functions which are $2\pi$-periodic, one would wonder how to define a similar notion for functions which are L-periodic.

Assume that f(x) is defined and integrable on the interval [-L,L]. Set

\begin{displaymath}F(x) = f\left(\frac{Lx}{\pi}\right).\end{displaymath}

The function F(x) is defined and integrable on $[-\pi, \pi]$. Consider the Fourier series of F(x
\begin{displaymath}F(x) = f\left(\frac{Lx}{\pi}\right) \sim \frac{a_0}{2} + \sum_{n=1}^{\infty} \Big(a_n\cos(nx) + b_n\sin(nx)\Big).\end{displaymath}

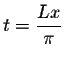Using the substitution $t =\displaystyle \frac{Lx}{\pi}$, we obtain the following definition:

Definition. Let f(x) be a function defined and integrable on [-L,L]. The Fourier series of f(x) is

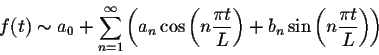
\begin{displaymath}f(t) \sim a_0 + \sum_{n=1}^{\infty} \left(a_n\cos\left(n\frac{\pi t} {L}\right) + b_n\sin\left(n\frac{\pi t}{L}\right)\right)\end{displaymath}

where
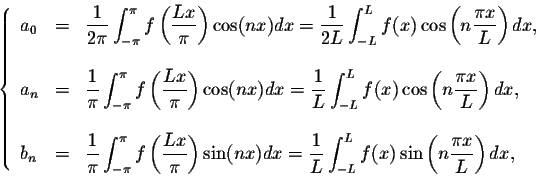
\begin{displaymath}\left\{\begin{array}{lclr} a_0 &=& \displaystyle \displaystyl... ...f(x) \sin\left(n\frac{\pi x}{L}\right)dx,\\ \end{array}\right.\end{displaymath}

for $1\leq n$.

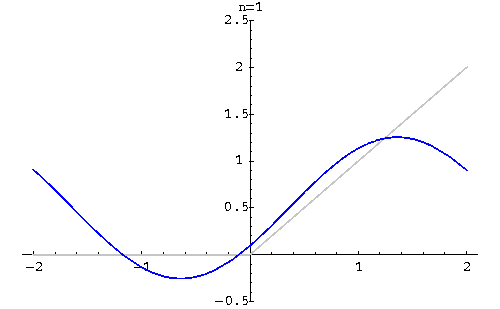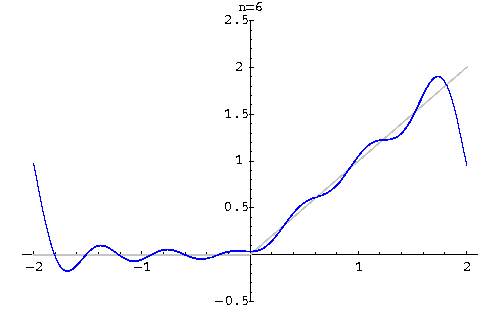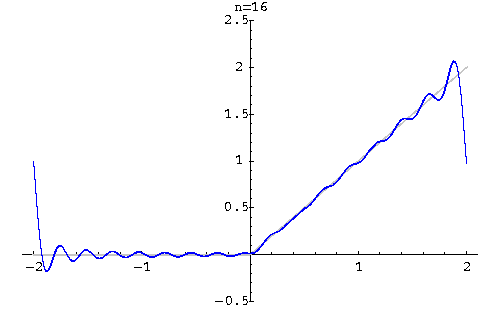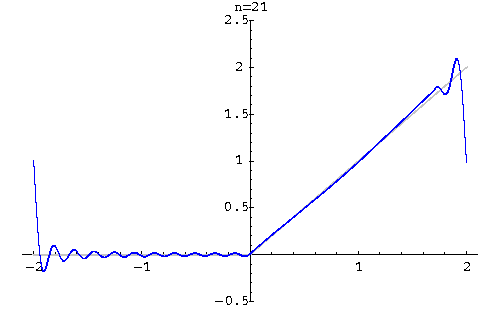
Example. Find the Fourier series of

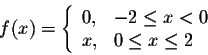
\begin{displaymath}f(x) = \left\{ \begin{array}{lll} 0,& -2 \leq x < 0\\ x, & 0 \leq x \leq 2 \end{array} \right.\end{displaymath}

Answer. Since L = 2, we obtain
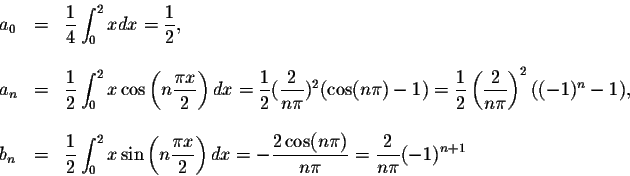
\begin{displaymath}\begin{array}{lll} a_0 &=& \displaystyle \frac{1}{4} \int_{0... ...{n\pi} = \displaystyle \frac{2}{n\pi}(-1)^{n+1}\\ \end{array}\end{displaymath}

for $ n \geq 1$. Therefore, we have
\begin{displaymath}f(x) \sim \frac{1}{2} + \sum_{n=1}^{\infty} \left[\frac{2}{n... ...rac{2}{n\pi}(-1)^{n+1}\sin\left(n\frac{\pi x}{2}\right)\right].\end{displaymath}

M.khosraviani دوشنبه 25 آذر 1392 ساعت 20:26
نظرات 0 + ارسال نظر
برای نمایش آواتار خود در این وبلاگ در سایت Gravatar.com ثبت نام کنید. (راهنما)
ایمیل شما بعد از ثبت نمایش داده نخواهد شد